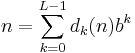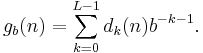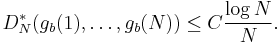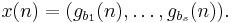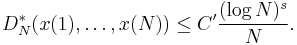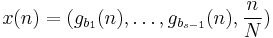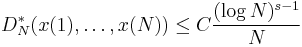Constructions of low-discrepancy sequences

There are some standard constructions of low-discrepancy sequences.

Contents

The van der Corput sequence

Main article: van der Corput sequence

Let

n=\sum_{k=0}^{L-1}d_k(n)b^k

be the b-ary representation of the positive integer n ≥ 1, i.e. 0 ≤ dk(n) < b. Set

g_b(n)=\sum_{k=0}^{L-1}d_k(n)b^{-k-1}.

Then there is a constant C depending only on b such that (gb(n))n ≥ 1 satisfies

D^*_N(g_b(1),\dots,g_b(N))\leq C\frac{\log N}{N}.

where D*N is the star discrepancy.

The Halton sequence

Main article: Halton sequence

The Halton sequence is a natural generalization of the van der Corput sequence to higher dimensions. Let s be an arbitrary dimension and b1, ..., bs be arbitrary coprime integers greater than 1. Define

x(n)=(g_{b_1}(n),\dots,g_{b_s}(n)).

Then there is a constant C depending only on b1, ..., bs, such that sequence {x(n)}n≥1 is a s-dimensional sequence with

D^*_N(x(1),\dots,x(N))\leq C'\frac{(\log N)^s}{N}.

The Hammersley set

Let b1,...,bs-1 be coprime positive integers greater than 1. For given s and N, the s-dimensional Hammersley set of size N is defined by

x(n)=(g_{b_1}(n),\dots,g_{b_{s-1}}(n),\frac{n}{N})

for n = 1, ..., N. Then

D^*_N(x(1),\dots,x(N))\leq C\frac{(\log N)^{s-1}}{N}

where C is a constant depending only on b1, ..., bs−1.

References